DataGenetics has an excellent analysis of the children's game Chutes and Ladders, where the distribution of the number of moves needed to win the game is computed via a Monte-Carlo simulation. They also construct the state transition table, apply it to the starting state, and show the evolution of the player's position distribution over the first 100 turns.
In this post, we take a slightly different track, and use linear algebra to compute the expected number of turns to win from any square on the board. It takes an expected 39.6 turns to win from the starting position, and the results for the rest of the board are as follows. Note: in the DataGenetics post, the game rule stating that you must win on an exact count is ignored, because the author hates that rule. In this calculation, I've reinstated that rule, to keep the results in line with the official Hasbro version of the game.
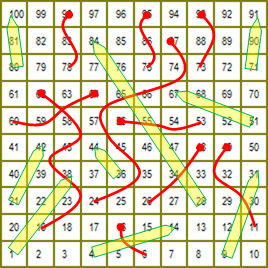
First, a diagram of the board, with thanks to DataGenetics:

And, the expected number of turns to win for each location:
| 0.0 | 6.0 | 20.5 | 10.8 | 10.8 | 18.7 | 12.1 | 20.5 | 16.6 | 15.9 |
| 25.6 | 24.5 | 23.5 | 22.6 | 21.6 | 20.9 | 34.7 | 17.6 | 17.8 | 16.8 |
| 0.0 | 20.6 | 20.5 | 20.1 | 19.6 | 18.7 | 17.6 | 20.5 | 20.5 | 15.9 |
| 25.2 | 35.6 | 22.2 | 25.9 | 20.4 | 20.4 | 20.4 | 20.0 | 19.8 | 19.8 |
| 25.9 | 26.9 | 27.9 | 28.3 | 29.2 | 28.2 | 28.7 | 29.2 | 29.6 | 20.4 |
| 33.9 | 34.1 | 34.7 | 33.9 | 31.9 | 31.6 | 31.3 | 35.1 | 38.6 | 28.6 |
| 34.4 | 34.8 | 35.3 | 35.5 | 33.9 | 35.6 | 35.9 | 36.2 | 36.4 | 36.6 |
| 34.1 | 33.8 | 34.3 | 34.7 | 34.9 | 35.1 | 35.3 | 22.6 | 37.3 | 36.8 |
| 35.5 | 35.6 | 35.7 | 35.8 | 39.5 | 37.0 | 37.5 | 37.8 | 38.2 | 38.6 |
| 35.3 | 40.1 | 39.6 | 37.5 | 39.7 | 39.5 | 39.2 | 39.0 | 36.6 | 39.1 |
A few observations. The value of the first ladder, which ascends from position 1 to 38, can easily be seen: the expectation value is lower on square 1 than on any other square in the first two rows. Similar patterns, of varying severity, occur wherever a ladder or chute starts. One oddity in this trend is the ladder ascending from 21 to 42. Taking it will help you only very little, because you will miss your chance to take the especially good ladder at 28, which ascends all the way to 84. Also striking to me is how little the EVs vary over the bottom half of the board. Not until square 50 does the EV drop below 30 turns, and this is doubtlessly due to the chutes on squares 48 and 49. (I invite the reader to confirm this by running the below code with those two chutes removed.) Getting past this pair of chutes is an important milestone towards winning. Finally, it surprised me that the EV is over 10 turns for almost every square on the board — only squares 80 and 100 (which are winning squares) and square 99, at an EV of 6, are anywhere close to winning.
Here's Octave code to compute the expectations:
boardsize = 100
matsize = boardsize + 1
maxroll = 6
chutes = [16, 6; 48, 26; 49, 11; 56, 53; 62, 19; 64, 60; 87, 24; 93, 73; 95, 75; 98, 78]
ladders = [1, 38; 4, 14; 9, 31; 21, 42; 28, 84; 36, 44; 51, 67; 71, 91; 80, 100]
# A matrix of transitions that describes the effect of rolling a die.
# Note: you must win on an exact count.
roll = zeros(matsize, matsize);
for i = 1:maxroll
roll += diag(ones(matsize-i, 1), -i);
endfor
for i = 0:maxroll-1
roll(matsize-i, matsize-i) = maxroll - i;
endfor
roll /= maxroll;
# A matrix of transitions that describes the effect of
# following the chutes and ladders.
follow = eye(matsize);
for i = 1:size(ladders, 1)
follow(ladders(i,1)+1, ladders(i,1)+1) = 0;
follow(ladders(i,2)+1, ladders(i,1)+1) = 1;
endfor
for i = 1:size(chutes, 1)
follow(chutes(i, 1) + 1, chutes(i, 1) + 1) = 0;
follow(chutes(i, 2) + 1, chutes(i, 1) + 1) = 1;
endfor
# Changing the rules slightly to allow following chutes and ladders
# both at the start and end of each turn will help give us a more
# sensible answer for squares that start a chute or ladder.
transition = follow * roll * follow;
# Equation we are going to solve:
# expected_turns - one = transition' * expected_turns
M = eye(matsize) - transition';
V = ones(matsize, 1);
# The last row of this equation is nonsensical, so replace it with a
# condition stipulating that the final entry of expected_turns is zero.
M(matsize, matsize) = 1;
V(matsize) = 0;
# Solve the equation
expected_turns = M^-1 * V;
# It doesn't take a turn to follow the ladder on square 80, because
# you don't have to roll afterward. So set expected_turns to zero
# for this square.
expected_turns(80 + 1) -= 1;
# Annotate the results and display.
expected_turns = [(0:100)', expected_turns]